Estamos viviendo un período electoral, el interludio entre las PASO y las elecciones generales. En la casa, en los bares y en las redes arrecian las discusiones del momento: ¿cuál es el/la mejor candidato/a ¿Quién dijo la verdad y quién mintió en campaña? ¿Cómo se te ocurre votar a tal?
Imaginemos. Después de un asado, un señor con su sobrina discuten qué sectores apoyan a tal o cual partido. La sobrina argumenta que las prioridades de las personas jóvenes no son las mismas que las de las mayores. Hay que votar por alguien que incorpore una agenda joven a su plataforma. El señor prefiere al candidato del partido A (Armando, pongamos), mientras que la sobrina prefiere a la candidata del partido B (Bárbara, pongamos), porque entiende que es la que mejor interpreta las necesidades de los jóvenes.
El señor esgrime una encuesta: “Busquemos datos. En vez de discutir sobre qué creemos que le gusta a la mayoría, nuestras decisiones se tienen que basar en información”. En ese estudio, Armando es el favorito tanto en el segmento de jóvenes como en el de mayores. La sobrina agarra la misma encuesta y dice: “¡claro, pero Bárbara es la favorita si consideramos a todos!”.
Antes de tirar este artículo pensando que no tiene sentido o que el señor y su sobrina habían bebido de más, vayamos a ver los números. Esta situación, de hecho, es bastante frecuente: algunas encuestas no entrevistan a la misma cantidad de personas de cada grupo o segmento. Es posible que las personas sean consultadas por varias preguntas o solo algunas. O que puedan elegir múltiples respuestas. En otras palabras, la manera en la que están conformadas las muestras determinará los resultados. El señor y su sobrina pueden tener ambos la razón.
Paradoja: ese oscuro objeto de la razón
En este ejemplo imaginario pensamos en la realización de consultas sobre la aceptación de un conjunto de candidatos/as, entre quienes se encuentran Armando y Bárbara. En cada encuesta las consultas se ordenaron de manera aleatoria y se hicieron tantas encuestas como fueran necesarias, hasta obtener 2200 respuestas para cada candidato/a (no todas las personas respondieron por todos los/las candidatos/as).
Los resultados de las consultas arrojaron que de las 2200 personas que contestaron por el candidato A, un 55% dijeron que les gusta; mientras que de las 2200 que contestaron por B, este porcentaje aumenta a 65%. Bárbara es la más aceptada si consideramos las proporciones totales.
Sobre las edades de las personas encuestadas, se observa que entre los adultos consultados por A, el 51% manifiesta aceptación, mientras que entre los adultos consultados por B ese porcentaje es de solo el 40%. Por otra parte, entre los jóvenes consultados por A, el porcentaje de aceptación es del 91%, y entre los jóvenes consultados por B, esa proporción se reduce a 80%. Tanto en el segmento de jóvenes como en el de adultos, Armando es favorito.
Esto se refleja en la siguiente tabla, que respalda igual de bien a las afirmaciones del tío y la sobrina. Pero entonces, ¿quién tiene razón?

Esto se llama la paradoja de Simpson y puede darse en muchas situaciones, induciéndonos a pensar que estamos “siguiendo los datos”. En realidad, los datos nos pueden llevar a conclusiones distintas dependiendo de la forma en que los agrupemos. Y en algunos casos esas conclusiones pueden ser erróneas cuando intentamos responder a preguntas específicas.
Esse est percipi: ¿Los datos son o los datos son en tanto desagregados?
Lamentablemente, no se trata sólo de un juego intelectual: este efecto tiene consecuencias en la realidad y en algunas ocasiones de forma notoria. En 1973, la Universidad de UC Berkeley analizó los números de sus ingresantes para ver si existía un sesgo de género. Encontraron que de 8442 aplicantes hombres, un 44% era admitido, mientras que de las 4321 aplicantes mujeres, solo un 35% eran admitidas. La posibilidad de que esto fuera casualidad era bajísima (estadísticamente, p 10-26). En consecuencia, había altas chances de terminar con un juicio por discriminación.

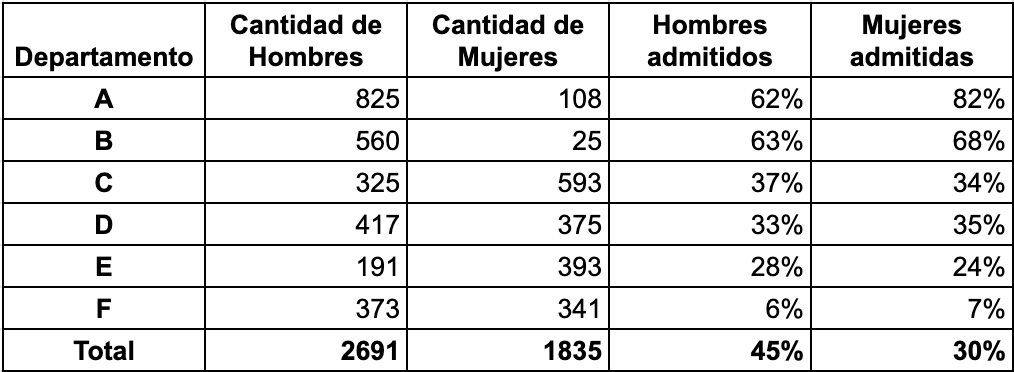
Un profesor de estadística decidió examinar los datos con cuidado, desarmando el agregado y mirando la información en contexto. La conclusión fue terminante: no hay sesgo si uno analiza por separado los Departamentos en los que se presentaron las personas que aplicaron. Lo que sucedía era que había más mujeres aplicantes a departamentos con mayores restricciones de ingresos (Departamento F) y menos mujeres aplicantes a departamentos con mayor tasa de aceptación (Departamento A). A pesar de tener una tasa de aceptación superior en la mayoría de los departamentos, las mujeres se veían en desventaja en términos agregados por la gran cantidad de rechazos en los departamentos donde más intentaron ingresar.
Por supuesto, esto no anula la posibilidad de que existiera discriminación. De hecho la educación y las presiones sociales llevan a las mujeres a ocupar determinados roles y carreras. Pero eso no surgía de los porcentajes de aceptación e ingreso a los Departamentos. La tabla completa puede encontrarse en varios lugares como ejemplo de la paradoja de Simpson, a continuación se ve la tabla para los 6 departamentos con más alumnos.
La pugna por los doce hombres en pugna
En septiembre de 1993, el Departamento de Justicia de Nueva Zelanda inició un estudio sobre la composición de los jurados. La sospecha era que la comunidad Maorí, que ha sufrido históricamente segregación en ese país, estaba subrepresentada en los jurados selectos. El Departamento de Justicia presentó los números a nivel nacional: las personas maoríes representaban el 9.5% de la población total y el 10.1% del grupo de potenciales jurados a nivel nacional. Esto daba por cerrado el tema. De hecho, los maoríes estaban sobrerrepresentados.
Nuevamente, un investigador no se conformó con tener información agregada y decidió dar un doble clic a los datos. Al mirar el detalle distrito por distrito, usando la información del censo para conocer la proporción de maoríes por grupo etario en cada comunidad, encontró que los maoríes estaban subrepresentados en cada uno de los distritos observados. A nivel agregado, los maoríes parecían estar sobrerrepresentados en el grupo de potenciales jurados. En cambio, a nivel distrito, se encontraban sistemáticamente por debajo del porcentaje de población factible de ser electo.

La paradoja de Simpson explica este resultado contraintuitivo, en el cual los resultados o tendencias observadas a nivel agregado cambian de signo cuando el grupo general se divide en otros más pequeños.
En este caso, el tamaño del grupo de potenciales jurados no es proporcional a la población de cada distrito. En particular, en los distritos con alta proporción de maoríes (Rotura y Gisborn, por ejemplo) tiende a haber grupos de potenciales jurados relativamente grandes. Por lo tanto, a pesar de estar subrepresentados cuando se evalúa distrito por distrito (Rotura: 27% de población elegible y 23.4% de maoríes seleccionados como potenciales jurados; Gisborne: 32.2% de población elegible y 29.5% de maoríes seleccionados como potenciales jurados), la cantidad de maoríes seleccionados en ellos contribuye a hacer más grande la proporción que se verifica a nivel agregado.
La tablita de Mr. Ford
Agrupar datos en forma descuidada y tener categorías heterogéneas puede llevar a tener evidencia a favor y en contra de un argumento con los mismos datos. Durante la presidencia de Gerald Ford, entre 1974 y 1978, este republicano conservador tuvo la política de mantener o bajar los impuestos para cada grupo de ingresos. Sin embargo, también logró subir la presión impositiva total. ¿Cómo lo hizo?

La explicación es muy sencilla: 1974-1978 fue un período inflacionario en Estados Unidos y por lo tanto mucha gente pasó de categoría impositiva por este motivo. Mientras que para las primeras tres categorías impositivas el porcentaje del impuesto y la base imponible se redujeron, en las categoría 4 y 5, a pesar de haberse reducido (mínimamente) el porcentaje del impuesto, la base imponible aumentó un 84.04% y 113.43% respectivamente, lo cual contribuyó a incrementar el total recaudado y el porcentaje de recaudación sobre los ingresos totales.
Nuevamente, la información agregada muestra resultados inversos a la que se puede obtener cuando se incorpora una nueva variable que conforma subgrupos a partir del agregado: jóvenes y adultos en el ejemplo de votación, los distritos de Nueva Zelanda en el caso de la comunidad maorí, los departamentos de la U. Berkeley y las categorías impositivas en este último ejemplo.
Mientras mirás los nuevos datos, vos ya sos parte del padrón
Es muy importante tener en cuenta cómo se agrupan los datos cuando los grupos no son homogéneos. La paradoja de simpson nos muestra que la forma de agrupar puede esconder variables de importancia para el análisis o situaciones heterogéneas cuyo efecto puede quedar desdibujado, como vimos en el caso de los impuestos.
En todos los casos en que aparece este problema, subyacen relaciones causales complejas entre las variables que están ocultas en la agregación de los datos. El primer paso entonces es no esconder la heterogeneidad dentro de un agregado, sino analizar cada grupo por separado. Sin esto, no podremos identificar aquellas variables causales que explican las diferencias en los resultados y resuelven la paradoja.
Por otra parte, en el caso de las encuestas es clave entender cómo se consiguieron los datos, de dónde salen y qué motiva a alguien a responder. Como dice un viejo chiste: “hicimos una encuesta con una única pregunta: ¿Ud. responde encuestas o no? Y estamos muy contentos con el resultado: un 99% de las personas respondió que sí”. Por supuesto: las que no responden no están contadas. Habría que entender qué pensaba ese 1% o si se trata de un error de conteo.
Es crucial no tomar los datos como palabra divina o como una nueva religión: no lo son y no lo serán. Los datos alimentan el razonamiento, no lo reemplazan. Volviendo a nuestro ejemplo imaginario, ¿quién es el candidato que representa mejor el voto joven? La respuesta es simple: aquel con las mejores propuestas.
Fuentes
[1] Bickel P.J., Hammel E.A. and O’Connell J.W. (1975). “Sex Bias in Graduate Admissions: Data From Berkeley”
[2] Ian Westbrooke. (1998). “Simpson’s Paradox: An Example in a New Zealand Survey of Jury Composition”
[3] Ooi, Yao Hua. (2004). «Simpson’s Paradox – A Survey of Past, Present and Future Research» . Wharton Research Scholars. 15. https://repository.upenn.edu/wharton_research_scholars/15/
[4] Pearl, Judea. (1999).“Simpson’s paradox: An anatomy” . Computer Science Department, University of California, Los A|ngeles. http://bayes.cs.ucla.edu/R264.pdf
[5] Wagner, C. H. (1982). “Simpson’s Paradox in Real Life”. The American Statistician, 36 (1), 46–48. https://doi.org/10.2307/2684093
Agradecemos al Dr. Osvaldo Gonzalez quien señaló un error en una versión anterior de este artículo.
